by Nick Foukal, graduate student at Duke University
As the RAPID team prepares to release the next 18 months of AMOC measurements from the mooring array at 26°N, I have been busy building a statistical model to predict those observations. Statistical models extrapolate into the future using data on past states of the system and differ from physical models in that there is no dynamical constraint placed on the predictions. Whereas physical models might demonstrate how the AMOC responds to wind and air/sea buoyancy fluxes and build predictions based on that information, statistical models only need to know what the system has done in the past to predict the future. So in many ways, statistical models are not as useful as physical models; they cannot tell you why a system behaves the way it does, or how future changes to the environment may affect the system, but oftentimes statistical models can tell you the minimum amount of information you need to make accurate predictions.
Another useful trait of statistical models is that they provide a baseline metric from which to judge the performance of physical models. Weather forecasting is an example of this: until advances in computational capability and the advent of continuous satellite measurements improved the numerical weather forecasting models, the best-performing weather forecast models were statistical models. My goal in this project is to evaluate where oceanography is on the journey toward predictive skill: can physical models outperform a relatively simple statistical model in predicting the next 18 months of the AMOC?
State-space analysis is one of many ways to build a statistical model. The basic tenet of the state-space model that I use here is that the future state is a function of the current state. This type of state-space analysis also requires stationarity in the system, thus trends or oscillations with periods longer than the period of measurement must be removed. In addition, autocorrelation and known oscillations at periods shorter than the period of measurement should also be removed (if the oscillations are assumed to be stationary into the future) so that the state-space model can focus on the ‘unpredicted’ aspect of the data.
Given these requirements, I downloaded ten years of RAPID data (April 2004 – March 2014) at 12-hourly resolution, averaged the data to 10-day resolution due to the 10-day time scales of flow compensation between the upper and lower limbs of the AMOC as reported in Kanzow et al. [2007], calculated the integral auto-decorrelation time scale (36 days) and then averaged the data at 40-day resolution to produce a time series of independent observations. To remove the seasonal cycle, I calculated a continuous seasonal climatology (Fig. 1) by taking a 30-day running mean of the data padded with the December data at the beginning and the January data at the end. This padding ensured that the climatology was not biased by when the year began and ended and the running-mean ensured that the climatology was a continuous function rather than based on monthly means.
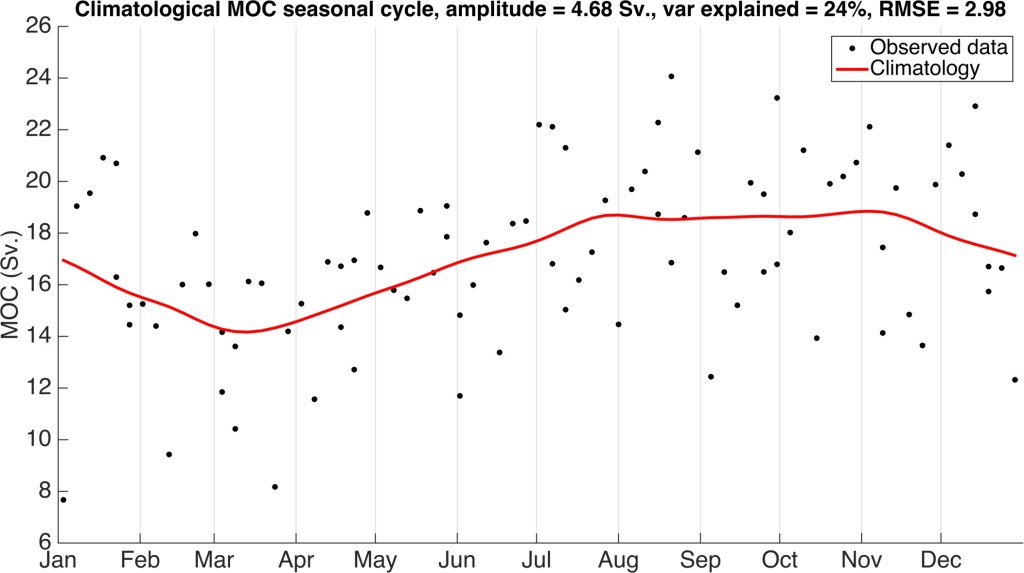
Figure 1. The climatological seasonal cycle of the RAPID AMOC data (2004-2014). The seasonal cycle has an amplitude of 4.68 Sv., RMSE of 2.98 Sv. and explains 24% of the variance in the data. The minimum occurs in March and there is a broad maximum from July through November.
To analyze trends or oscillations beyond the study period, I fit the data with five models: a linear trend line, a step-function with the mean from April 2004 to April 2008 and the mean from May 2008 to March 2014 (based on results from Smeed et al. [2013]), two linear trend lines for the same time periods as the step function, a quadratic fit, and a sine curve. The fit with the lowest RMSE is the sine curve (Fig. 2).
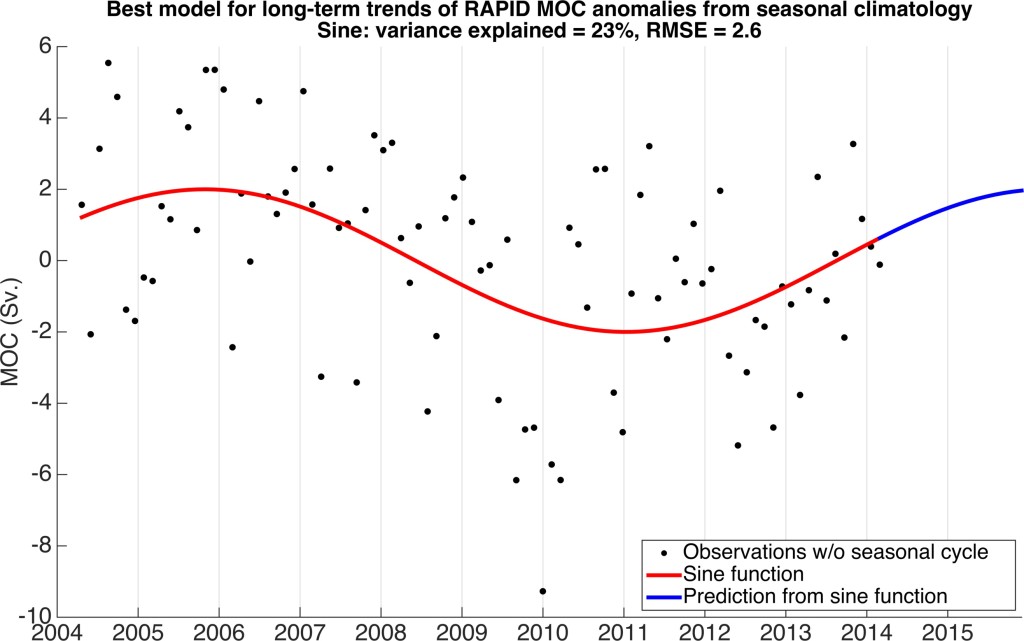
Figure 2. The sine curve fit to the AMOC observations without the seasonal climatology. The sine curve has an amplitude of 2 Sv., period of 10.41 years and phase shift of 6.16 years. This sine function has the lowest RMSE (2.6 Sv.) when compared to a linear fit, a step function fit (2004-2008 and 2008-2014), a quadratic, and two linear fits (2004-2008 and 2008-2014). The maximum of the sine curve occurs at the end of October 2005 and the minimum occurs in early January 2011. The next maximum predicted by just this component is in the Spring of 2016 while the most recent inflection point occurred in mid-2013.
To predict the AMOC signal that remained after the seasonal and long-term oscillations were removed, I fit the parameters of a state-space model to the ten years of anomalies (Fig. 3). The two parameters that require optimization are the number of dimensions and the number of nearest neighbors. Dimensions refers to the number of previous observations in time to use in the prediction, and the number of nearest neighbors refers to the number of time periods with similar AMOC variability (each consisting of the number of dimensions) to use. I tested models with zero to 25 dimensions and zero to 25 nearest neighbors by calculating each of the models’ RMSE when compared to the observations for the MOC observations from 2004-2014. The model with the lowest RMSE (2.46 Sv) has 10 dimensions (each prediction uses information from the past 400 days), and 14 nearest neighbors. The fact that the model needs just over one year of previous data implies that there may be residual seasonality that the seasonal climatology did not remove.
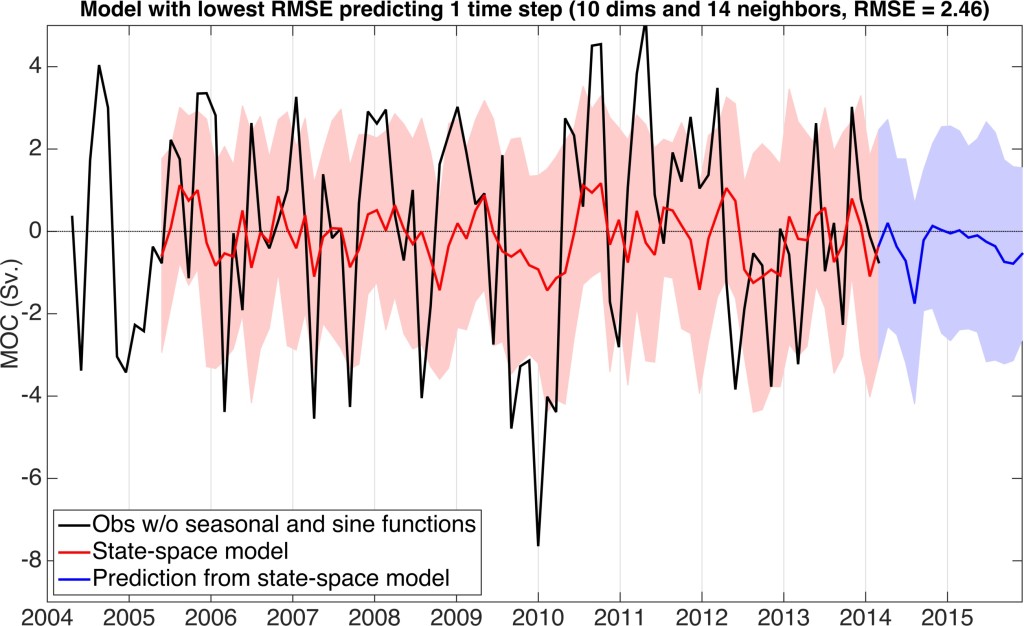
Figure 3. The state-space model fit to RAPID AMOC observations without the climatological seasonal and sinusoid cycles. The model uses 10 dimensions (400 days) and 14 nearest neighbors. State-space models with many nearest neighbors typically under-predict the amount of variance in the original data because the number of values that are averaged to create a prediction is too large.
When the three components (seasonal cycle, long-term oscillation and state-space model) are combined (Fig. 4), they recreate 48.5% of the variability in the observations from 2004-2014 and have a cumulative RMSE of 2.46 Sv. In comparison, models with just the mean MOC (RMSE = 3.42 Sv. and 0% of variance), the climatological seasonal cycle (RMSE = 2.98 Sv. and 23% of variance) and the climatological seasonal cycle plus the long-term sinusoid (RMSE = 2.60 Sv. and 42.1% of variance), do not fit the data as well. The combined model also produces a prediction for the next 18 months of the AMOC (Fig. 4, blue). Of the 6.11 Sv. amplitude in the predicted values, over 75% is due to the seasonal cycle, with the increasing sine component (Fig. 2, blue) slightly compensated by the negative state-space component (Fig. 3, blue). The two peaks in the combined model’s prediction (Fig. 4, blue) of 20.28 Sv. and 20.14 Sv. occur in October 2014 and August 2015, respectively, and the trough of 16.06 Sv. occurs in February 2015.
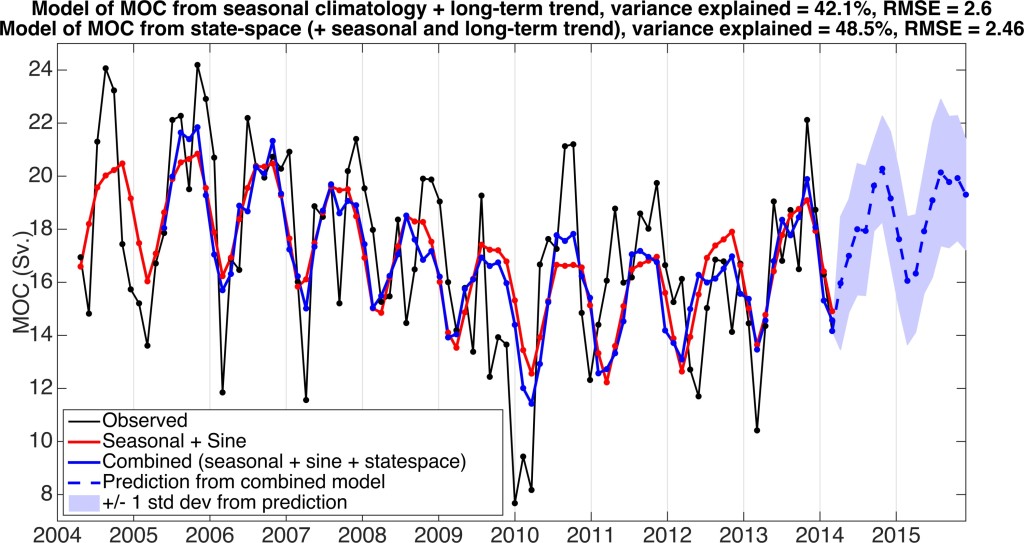
Figure 4. A comparison of statistical models with predictions for the next two years of RAPID AMOC based on the model that combines the seasonal, long-term and state-space models. The average standard deviation for the next two years (blue shading) is +/- 2.4 Sv. The error does not diverge because it depicts the amount of spread in each individual prediction of the next time step provided that the previous prediction was accurate.
References
Kanzow, T. et al. (2007) Observed Flow Compensation Associated with the MOC at 26.5°N in the Atlantic. Science, vol. 307, pp. 938-941.
Smeed, D. et al. (2013) Observed decline of the Atlantic Meridional Overturning Circulation 2004 to 2012. Ocean Science Discussions, vol. 10, pp. 1619-1645.